【2021年度】東工大数学で対策すべき分野と単元｜優先順位を紹介

今回は『【2021年度】東工大数学で対策すべき分野と単元｜優先順位を紹介』について説明したいと思います。

今回は、東工大の数学の過去問10年分を分析した結果と、東工大卒である私の考察をもとに2021年度の東工大数学の出題分野を推測してみました。

二次試験までに数学の勉強が間に合いそうにない人や、ヤマを張って勉強をしたい人は、ぜひ今回の内容を参考にしてみてください。

東工大の数学過去問10年分の出題分野

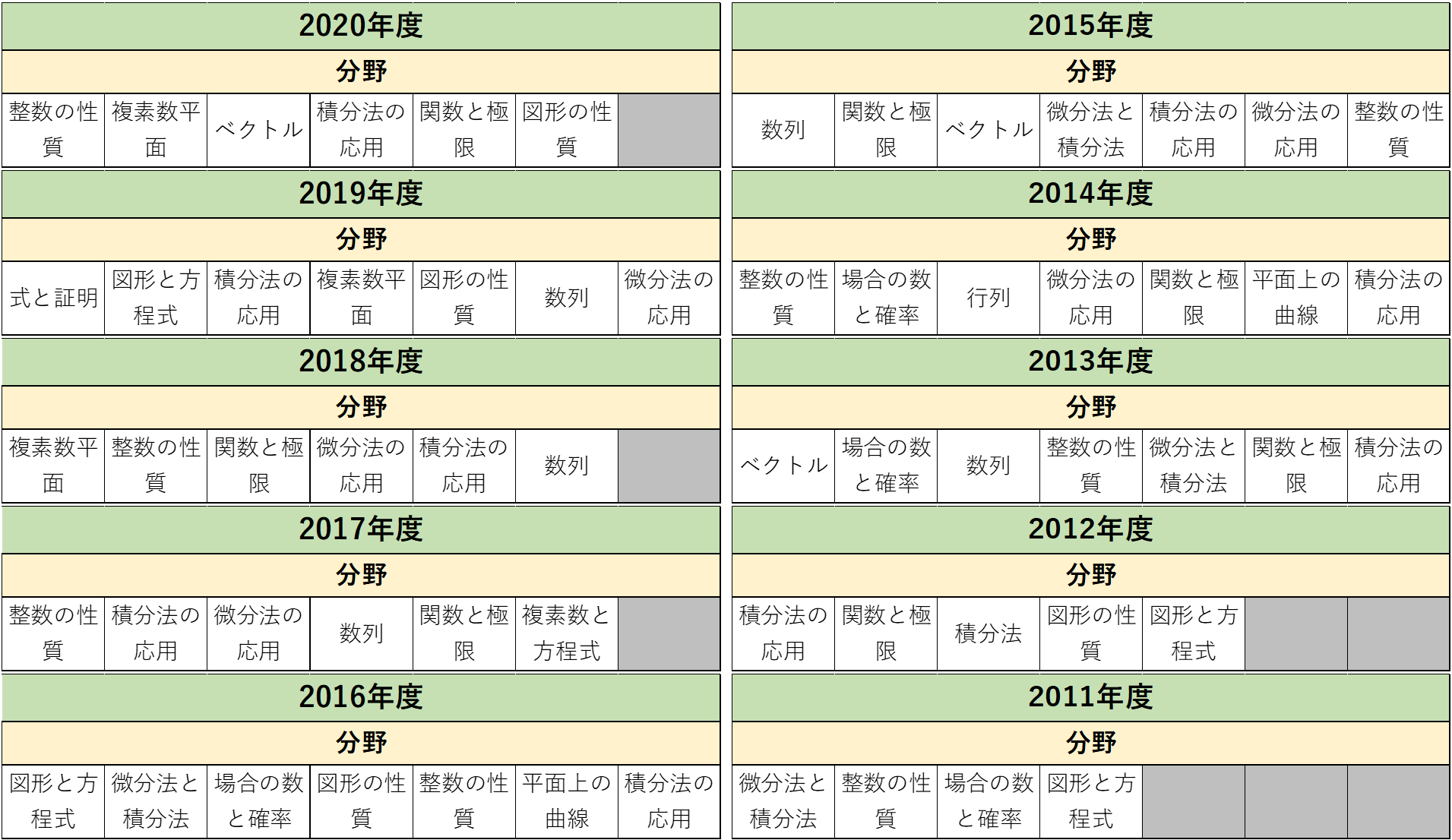
こちらは、2011年度から2020年度までの東工大の数学の出題分野一覧になります。

今回はこれらのデータをもとに、2021年度の東工大の数学の出題分野を推測してみました。

①過去10年間での各分野の出題頻度

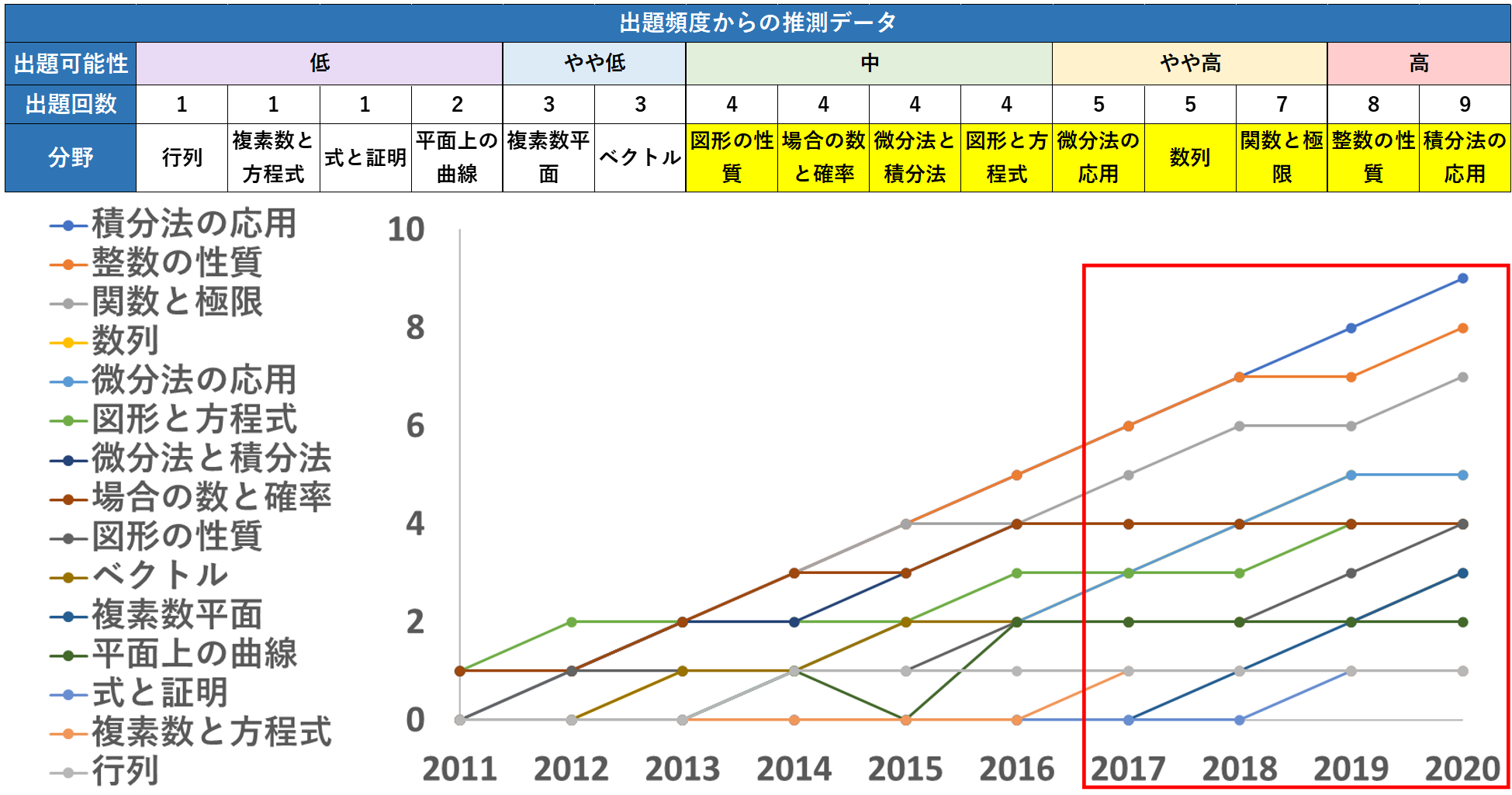
※白背景：出題頻度が少なく出る可能性も低い分野

※黄色背景：出題頻度が多く出る可能性も高い分野

「整数の性質」と「積分法の応用」に関しては、10年中9年も出続けているほど、高頻出の分野なので要注意です。

「図形の性質」「場合の数と確率」「微分法と積分法」「図形と方程式」に関しては、10年中4年しか出ていないのですが、出る可能性を視野に入れておいた方が良いでしょう。

グラフは、各分野の出題回数を年ごとに計測した推移グラフです。

注目するべき点は、赤枠で囲われた2017年度から2020年度までのチャートで、3年間のうちどれくらいの頻度で出題されたかの推移を表しています。

②直近3年での各分野の出題頻度

※白背景：出題頻度が少なく出る可能性も低い分野

※黄色背景：出題頻度が多く出る可能性も高い分野

「式と証明」「図形と方程式」は3年間で1回しか出題されていないので、注意は必要ですが出題される可能性はそれほど高くないでしょう。

そして黄色下線部の分野は、2021年度も出題される可能性が非常に高い分野となります。

例えば、「複素数平面」「積分法の応用」に関しては、直近3年間で毎年出ているので、おそらく来年も出題されると思います。

ここまでに紹介した2つの表を考慮すると、上図のような結論になります。

【結論】2021年度に出題される分野

入試まで時間がない人向けの勉強分野

時間がない人の場合は、上記5つの分野を優先的に学習してみると良いでしょう。

ただ、この方法は今のまま勉強していても合格の可能性が低い人が取るべきヤマの張り方なので、全分野対策しても入試に間に合う人の場合は、全分野対策しましょう。

東工大数学で対策すべき分野と単元の優先順位

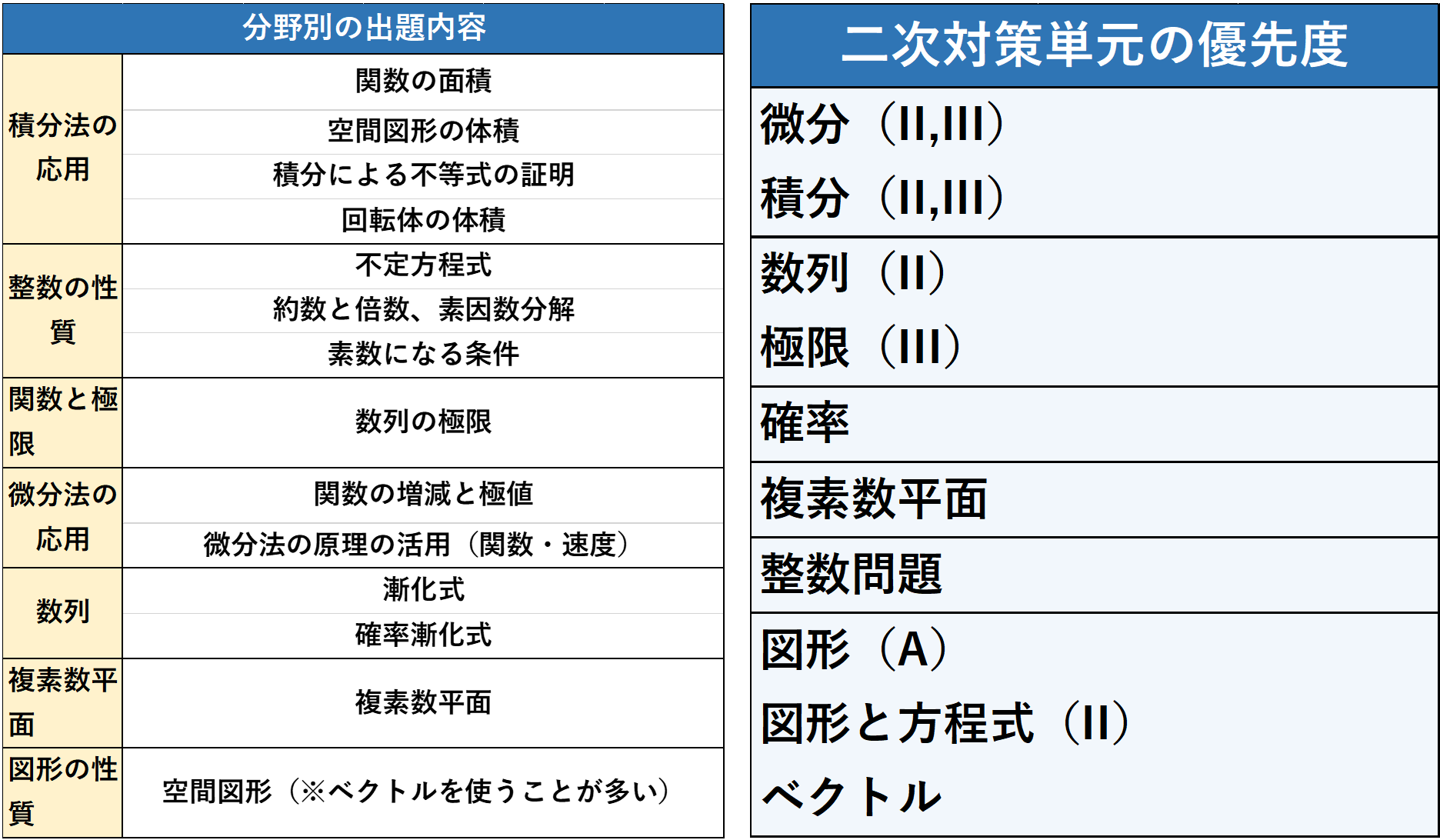
2021年度の東工大数学で出題される可能性が高い分野について、過去5年の問題内容をまとめました。

①出題上位の分野の問題内容

頻出度の高い7つの分野ごとに、今までに出題された問題内容の分類を載せているので、どんな問題に力を注いで学習すればいいかの判断軸として参考にしてみてください。

②東工大対策で優先して勉強すべき単元順

東工大入試まで時間がない受験生の場合は、上記の優先的に勉強すべき数学の単元を参考にしてみてください。

微分・積分

数II,III両方あるのですが、その両方の演習にかなり時間をかけて対策してください。

単純な面積や体積問題だけでなく、証明問題や大学範囲の数式の誘導問題などにも使われるので、かなり幅広い知識と応用力が必要です。

ほぼ間違いなくどちらかは出題されるので、入念に対策しておきましょう。

数列・極限

数Bの数列を完璧にしておけば、数IIIの極限の範囲はかなりスムーズにマスターできます。

特に、極限に関しては積分問題とも絡めて出題されることも多いので、東工大の数学の中ではかなり頻出度が高いです。

極限は一度マスターすれば応用もスラスラ解けるようになるので、ぜひ得点源にしてみてください。

確率

東工大の確率の問題は、最初の小問で共通テストに毛が生えたレベルの問題が出るか、あるいは確率漸化式の形で出るかです。

確率漸化式は一見難しそうに見えますが、慣れるとあれほど簡単なものはないので、ぜひ解法パターンを頭に入れておいてください。

たまに確率で特殊な問題が出ることがあるのですが、それほど注意しなくても大丈夫でしょう。

複素数平面

複素数平面は難易度は高いものの、それほど範囲が広いわけではないので、参考書を周回して対策すれば問題ないでしょう。

整数問題

整数問題は、「マスターオブ整数」という参考書で演習をしてある程度慣れておきましょう。

一つ一つが重厚な問題なので、全部は解かずにある程度頻出のパターンを定着させておくと、かなり苦手意識を払しょくできます。

図形・図形と方程式・ベクトル

数Aの「図形」数IIの「図形と方程式」、数Bの「ベクトル」に関してですが、これは東工大が大好きな「空間図形」の問題を解く時に必要になります。

空間図形は座標を設定することが多いのですが、その時にベクトルを使います。

そしてベクトルを使いこなすには、数Aの「図形」の知識と、数IIの「図形と方程式」の知識が必要になるので、東工大の空間図形の問題に対応するにはこの3単元を学習する必要があります。

以上が二次対策をする時の勉強すべき単元の優先度順です。

時間がない人は、ぜひ今回紹介した優先度を参考にしてみてください。

ただ、あくまで今回の推測は過去のデータと、私の主観がベースの推測なので、最後は自分で判断してみてください。