高校物理で微積は必要？｜難関大合格を目指す人向けに東工大卒が解説

今回は『高校物理で微積は必要？｜難関大合格を目指す人向けに東工大卒が解説』について紹介します。

理系の難関大志望の受験生は、一度は微積物理の存在を聞いたことがあるのではないでしょうか。

「微積を使うと物理がすごく簡単になる」「素早く式を組み立てて回答まで導くことができる」など、いい噂を聞いたことがあると思います。

物理は理系受験の”合格の鍵”になるので、ぜひ今回の内容を読んで参考にしてみてください。

【難関大志望向け】高校物理で微積は必要？

結論から言うと、微積物理は大学受験には一切必要ないです。

たとえ東大・京大・東工大のような理系の上位大学であったとしても、微積を使わないと解けない問題は出されません。

市販の参考書に載っている公式を使うことができて、問題文から現象の原理を読み取ることができれば、すべての受験物理の問題に対応することができます。

では、どうして有名予備校の物理講師が微積物理をオススメするのかについて、微積物理のメリットデメリットとともに紹介します。

微積物理のメリットとデメリット

微積物理のメリット

大学受験で出てくる物理の公式のほとんどは、大学範囲の微積分で導出されたものです。

そのため、微積物理を用いることで、公式の背景や原理を式から理解することができます。

そのため、一度マスターすれば色んな問題に対応することができ、「柔軟性」と「発想力」が格段に上がります。

また、公式を暗記していなくても、運動方程式のような基本式から多くの公式を導き出すことができるので、公式導出にも使えます。

そしてこれは難関大あるあるですが、大学範囲の問題を誘導つきで出してくることが多く、微積物理を用いた方が簡単に解けるケースも少なくありません。

微積物理のデメリット

微積物理の最大のデメリットは、習得するまでにかなりの時間を要する点です。

公式物理である程度の実力をつけて、原理や概念を理解できている状態であったとしても、最初はわけが分からなくて使いこなすまでに多くの時間がかかります。

そのため、多くの人はパターン化された問題しか解けないレベルで終わってしまうでしょう。

そして、パターン化された問題であれば慣れている公式物理で解いた方が圧倒的に早いので、中途半端な習得レベルでは微積物理はほとんど役に立ちません。

【実演】微積物理を使って問題を解く

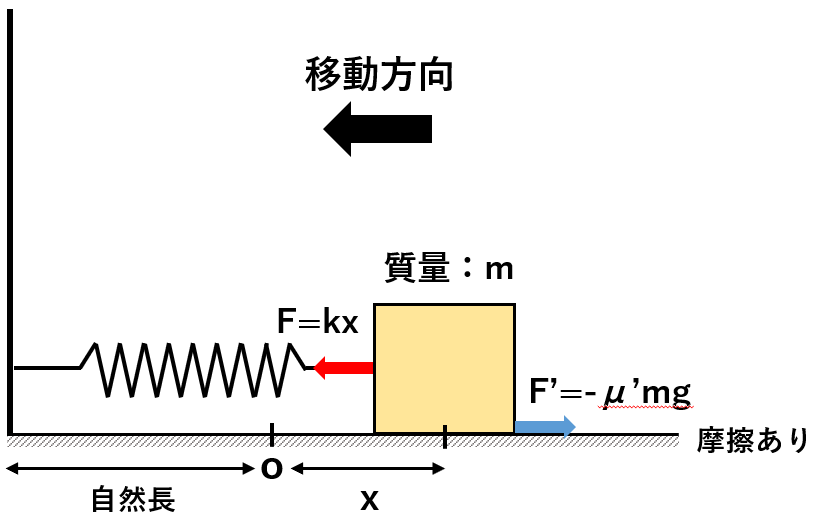
まず、「速度」と「加速度」の定義を微分で表してみます。下図をご覧ください。

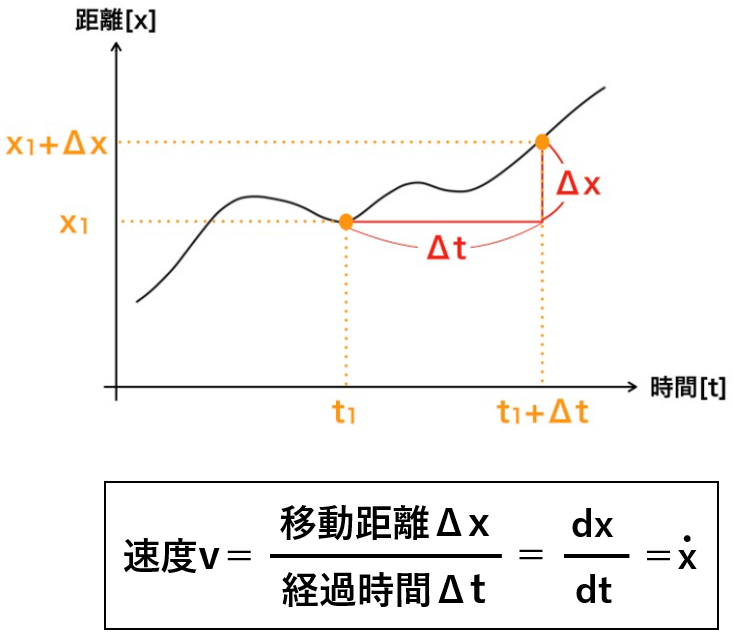
「速度」は、進んだ距離を経過した時間で割ったものなので、「移動距離Δx」を「経過した時間Δt」で割ったものが「平均速度」になります。

そして、速度の定義は「その瞬間での速さ」なので、速度は「変化量Δx」と「変化量Δt」を限りなく小さくしたもの、”dx/dt”で表されます。

そして、”dx/dt”を簡略化して書いたものが「xのシングルドット」です。

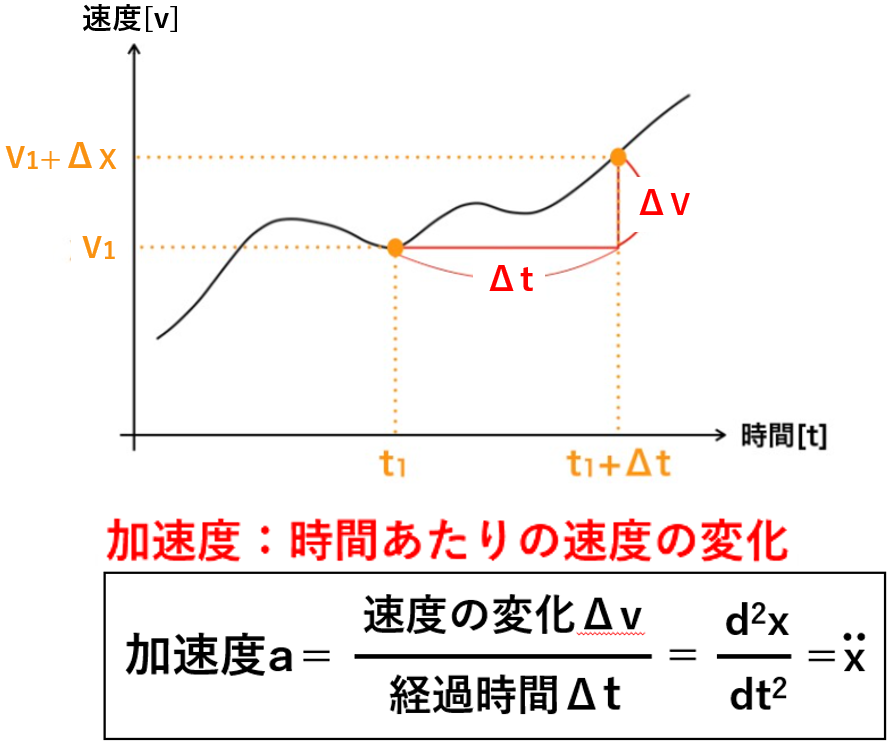
「加速度」は、時間あたりの速度の変化のことなので、「速度の変化Δv」を「経過時間Δt」で割ったもので表されます。

先ほどの速度の式（dx/dt）を代入すると、加速度は”d²x/dt²“で表され、これを簡略化すると「xのダブルドット」となります。

では、「速度」と「加速度」の関係を把握したところで、先ほどの問題を微積物理で解いてみましょう。

まず公式物理と同様に、運動方程式を立ててみましょう。

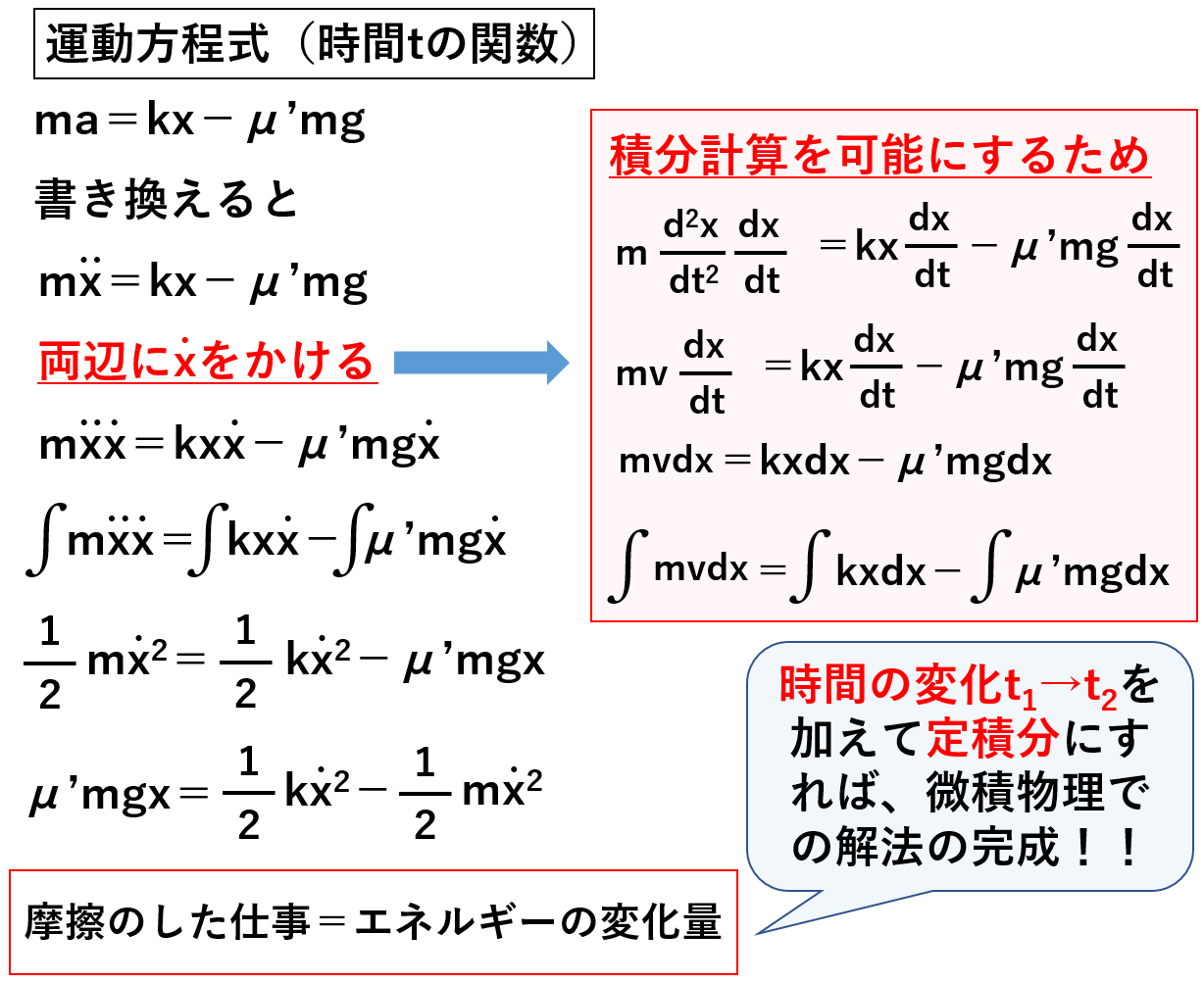
運動方程式を立てると、ma＝kx－μ’mgとなります。

この運動方程式を、先ほどの「速度」と「加速度」の表現に書き換えると、mx（ダブルドット）＝kx－μ’mgになります。

ここで、両辺にx（シングルドット）をかけてください。理由は、ピンク背景の欄に書いている通り、積分の計算を可能にするための式変形目的です。

両辺にx（シングルドット）をかけて積分をすると、1/2mx²（シングルドット）＝1/2kx²（シングルドット）－μ’mgxとなり、最終的に「摩擦のした仕事＝エネルギーの変化量」の式が完成します。

今回は”不定積分”で解いていますが、ここに時間の変化「t₁ → t₂」を”定積分”の範囲として用いれば、t₁の時の位置x₁、速度x₁（シングルドット）、t₂の時の位置x₂、速度x₂（シングルドット）で表現することができます。

このように、運動方程式さえ立てることができれば、あとは微積の計算テクニックだけで求めたい現象の式を導出できるのが、微積物理の強みです。

微積物理を習得するまでにかかる時間

これは私の経験ですが、私も受験生の頃に物理の点数を飛躍的に伸ばしたかったので、微積物理を独学で学んでいました。

その時に使っていた参考書が上で紹介したものになるのですが、正直マスターしたとは到底言えないレベルで終わりました。

この参考書自体は非常に分かりやすく、微積物理の原理の把握はできたのですが、難問題への応用となると途端に使い物にならなくなっていました。

たしかに、運動方程式などの基本的な式から答えまで微積で導出できた時は嬉しいですし、基本式さえ覚えていれば問題を解くことができるので非常に画期的なのですが、このレベルであれば公式物理で解いた方が早いです。

そして、微積物理をこのレベルまで使いこなすのに、4～5か月ほど要しました。

さらに、ここまで時間を費やしたにも関わらず、結局そのあとは公式物理で問題を解いて、微積物理を使うことはありませんでした。

【大学受験】微積物理の必要性まとめ

上記に該当する人以外は、基本的には微積物理をオススメできません。

もし学習するのであれば、完璧にマスターするまで学習するようにしましょう。

大学受験時における微積物理は、0か100のゲームのようなものです。

習得できなければほぼ役に立たず、逆に習得できれば飛躍的に物理力が上がります。

私の場合は途中で断念してしまいましたが、自信がある人は一度見てみるといいでしょう。