共通テストの数学で8割取れない人と取れる人の勉強法＆時間節約方法

今回は『共通テストの数学で8割取れない人と取れる人の勉強法＆時間節約方法』について紹介します。

まず最初に、共通テスト（センター試験）の数学は、センスや頭の良さ関係なしに、8割は誰でも取ることができます。

もし、どれだけ勉強しても8割を超えることができないと悩んでいる人は、単純に勉強法が誤っているだけの話です。

ぜひ今回の内容を参考に、共通テスト数学で8割を取って、数学を得点源にできるようにしましょう。

共通テスト数学で8割取れない人の勉強法

共通テストの数学で8割取れない人としては2タイプいます。

タイプ1の勉強例

例えば、問題を見てわかる兆しがないのに時間をかけて考える人や、解答を見て理解できる予感がしないのに考える人が該当します。

知識がないうちから理解して進めようとしても、非常に時間がかかってしまいます。

そうなると、受験は期間が決まっているので、目標を達成できない可能性が出てきます。

つまり、演習量不足になる可能性が高いということです。

そのため、長くて3～5分考えて分からなければ、すぐに答えを見てください。

8割を取れない段階の実力であれば、長いこと時間をかけて考えるだけ無駄です。

例えば、ジグソーパズルを想像してみてください。

まだ1ピースしか埋めていないパズルで「全体の絵を想像しろ」と言われても、分からないですよね。

ある程度ピースを埋めることができて初めて、全体の絵の候補を絞っていくことができます。

数学もパズルと同じで、知らない知識の問題を考えたところで誤った解釈をしてしまうだけなので、8割に満たない人の場合は3分ほど考えて分からなければ、解答を見て暗記をするようにしましょう。

タイプ2の勉強例

先ほどは「暗記をしない人はダメ」、今度は「暗記に頼りきりの人はダメ」と説明されて、困惑している人も多いと思います。

ここが数学の勉強の難しいところなのですが、暗記が必要なタイミングと、暗記から原理の理解に移るタイミングがあります。

ジグソーパズルで例えると、ピースがある程度そろったら、はめ込む作業だけじゃなく絵を想像する作業も必要ということです。

もしこれをしないと何が起きるかというと、解いたことのある問題は解けるのに、それ以外には対応ができなくなります。

共通テスト数学で8割取れる人の勉強法

参考書を変えて演習するメリットは、暗記した知識を自分で考えて使ったり、その知識の原理を自分で無意識的に考えられる点です。

同じ解法の問題でも色んなパターンの問題文があるので、そのパターンを頭に入れることができれば適応力が身についてきます。

そしてこれを繰り返すことで、いわゆる一般的にいう「応用力」が身に付きます。

共通テストの数学で時間節約する方法を実践

たとえば、これは共通テストの試行テストなのですが、センター試験と共通テストの大きな違いは文章量です。

この文章量のせいで解く時間が減ってしまうという人も多いと思います。

そのため、時間短縮をするためには、いかにして文章を読む時間を減らすかが重要になってきます。

共通テスト数学で時間短縮実践①

問題を見てみると、「図」と「長い文章」がついています。

この問題を見た時に最初にすることは、「長い文章」を読み始めるのではなく、設問から読むことです。

まずは設問の指示通り、図1を見ましょう。

図1を見ると、「aの値と頂点を設定しながら問題を解いていくのだろう」と理解ができますよね。

何をするかがイメージ出来たら、次は実際に問題を解くための指示に従って、f(x)＝0の解について書いた選択肢を選びましょう。

図1から見て分かる通り、xの負の領域でx軸と二点で交わっているので、異なる二つの負の解を持つ①が答えと分かります。

この問題（先ほどの続き）も、まずは設問の穴埋め前後を読んで指示を把握し、それから条件文である操作A, P, Qを読みましょう。

「エ」に関しては、x軸より上に放物線が収まればいいので、頂点のy座標であるqだけx軸より上に移動させればOKです。

「オ」に関しては、x軸より下に放物線が収まっていればいいので、aの値を負に変えるだけでいいということになります。

なので答えはそれぞれ「エ」③と「オ」①です。

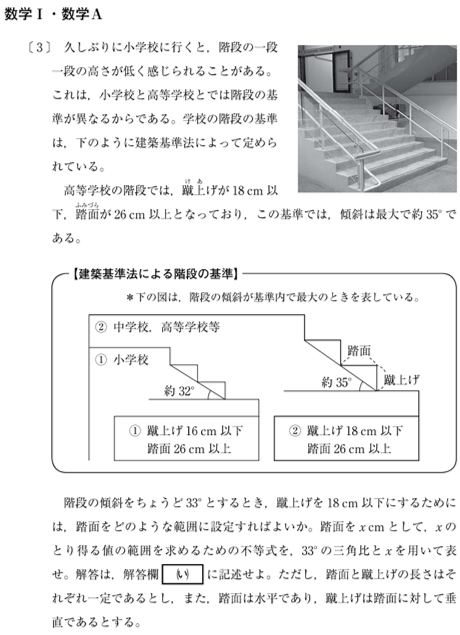
こちらも文章が長いので、この問題もまずは設問から読みましょう。

この問題は、あとは図②を見るだけで解けます。

まずは蹴り上げの高さをyと置くと、y≦18ですよね。ここでtanを用いると、tan33°＝y/xとなり、x＝y/tan33°になります。

Xは26以上と書いてあり、yは18以下なので、xの範囲は26≦x≦18/tan33°となります。

このように、共通テスト数学は無駄に長い文章が付けられていて、一見すごく時間がかかりそうに見えますが、実は文章のほとんどが問題を解くために必要ないです。

なので、共通テスト数学の時間を短縮して節約したければ、まずは設問を読んで、その次に図を見て、この2つの材料から必要な指示にだけ従うようにしましょう。

共通テストの数学で失敗しない方法

これは本当に重要で、一歩誤ると8割を取る実力があったとしても5割ほどになってしまうこともあります。

私が受験生の時も、センター試験の第二問目で超難問が出て、高得点保持者たちがこぞって5割を叩き出した事故が起きました。

そのせいもあり、その年のセンター数学の平均点は30点台でした。

高得点を取らないといけない人ほど、自分にプレッシャーをかけてしまって時間を大幅にロスしてしまい、他の問題に時間をかけられずに点数を失ってしまいます。

これは周りからよく言われることだとは思いますが、本当に起き得ることなので、ぜひ気をつけてください。