今回は「数学の偏差値を30上げる参考書ルートと勉強法」を、学年最下位から東工大に合格した筆者の経験をもとに紹介します。もしこの記事の内容をこなすことができたら、数学の偏差値が大幅に上がっているはずです。
目次
数学の勉強で大切なのは、どの期間で何をどれくらい反復するかです。ここで皆さんに質問ですが、数学にセンスは必要だと思いますか。
正解は、数学にセンスは必要です。ただ、ここでいうセンスとは生まれつきの才能のことではありません。センスとは、いかに知識を使いこなせるまで実践を重ねたか、つまりいかに泥臭い努力をしかです。
では、その泥臭い努力とはなにか。それが、先ほど紹介した「どの期間で何をどれくらい反復するか」です。

ここではまず参考書1周分終わらせることを目標にしよう
1. 達成するべき量
仮に達成するべきものが参考書1周分だとすると、達成するべき量はその参考書のページ数になります。
2. 自分の学習速度
参考書を進める時、1時間あたりの進み具合は人によって異なります。自分の場合はどれくらい進むのか、試しに測ってみてください。
3. かけるべき期間
達成するべき量と1時間あたりに進められる量が決まれば、達成までにかかる勉強時間が導き出されます。もし達成期間が決まっていれば、その日数で割ると1日の数学の勉強時間がわかるし、1日の数学の勉強時間が決まっていれば、達成にかかる期間がわかります。
| 参考書のページ数 | 300p |
| 1hで進むページ数 | 5p |
| 達成したい期間 | 20日 |
| 数学の勉強時間 | 1日3時間 |

数学初心者の場合は1日6時間ほど数学にかけると約3〜4週間で1周できるくらいが目安
1周目の計画が立てられたら、あとは2周目3周目と同様に勉強計画を立てることができるので、一番鬼門となるのは「参考書1周目」です。
あくまで経験則ですが、2周目は1周目の7割ほど、3周目は1周目の5割ほどの労力で反復することができるので、なんとか踏ん張って1周目を終わらせましょう。
数学が苦手な人の場合、気をつけなければいけない以下2つの注意点があります。
- 不明な問題はすぐ解答を見る
- 最初は暗記する意識で進める
すでに基礎力のある人が参考書で腕試しをするなら話は別ですが、基礎が身についていない数学苦手者が参考書を進める場合は、いくら考えたところで正解は浮かんできません。
もし数学初心者が早く成績を上げたいのなら、いかに早く基本的な解法パターンを頭に入れられるかがポイントになります。

でも、数学は根本原理の理解と応用力が重要ってよく聞くよね
はい、最終的には解法パターンの原理の理解と応用力が数学の得意不得意を分けます。しかし、それはやるべき基礎知識をつけてある程度訓練をした、ある一定レベルまで達した人がやるべき次のステップです。
なので、基礎知識がまだ身についていない人は、以下の手順に沿ってまずは基礎知識のインプットから始めましょう。
どのように解けばよいか10秒以内に方針が立たない場合はすぐに解答を見る
公式や定義がわからない場合は単元最初の説明箇所を覚え直し、解き方がわからない場合は解法を覚える
解法を覚えたら最後まで自力で解けるかもう一度解いてみて、解けるようになるまで繰り返す
自力で解けるようになれば、次の問題に進んで同様の作業を行う
この手順で参考書を進めれば、一時的な記憶として解法パターンが身につきます。ただし、前述の通りこれは一時的な記憶なので、2周目3周目と反復を重ねることでしっかりと定着させていく必要があります。
参考書2周目は、以下のように1周目の時と少し異なる立ち回りをします。
- 参考書2周目は思い出す作業
- 忘れている箇所は覚え直す
- 覚えている箇所は印をつける
参考書2周目は、主に1周目で覚えた内容を思い出す工程だと思ってください。当然、1周しただけではなかなか記憶が定着しないので、できない問題も多々あると思います。

2周目はつまらないと感じやすい工程なので忍耐する覚悟が大切
どのように解けばよいか30秒以内に思い出せない場合はすぐに解答を見る
自力で思い出して解けた問題には、問題文上のスペースに◯を1つつける
公式や定義がわからない場合は単元最初の説明箇所を覚え直し、解き方がわからない場合は解法を覚え直す
解法を覚えたら最後まで自力で解けるかもう一度解いてみて、解けるようになるまで繰り返す
自力で解けるようになれば、次の問題に進んで同様の作業を行う
2周目が完了すれば、参考書の半分ほどの解法が身についてきます。この段階で終わってしまうと、見たことはあるのに解けないという中途半端な状態で終わってしまうので、このあと3周目に入っていきます。
参考書3周目以降も基本的には2周目と同様ですが、以下の点が異なることに注意してください。
- 3つ◯がついた問題は一旦OK
- 全問題で◯が3つなら参考書OK
参考書3周目以降は解ける問題も多くなるので比較的スムーズに進みます。また、この頃から苦手意識も徐々に払拭されてきます。

3周目以降は徐々に空きが出てくるけどかなり大切な工程なのでもう少し耐えよう
どのように解けばよいか1分以内に思い出せない場合はすぐに解答を見る
自力で思い出して解けた問題には、問題文上のスペースに◯を1つつける
公式や定義がわからない場合は単元最初の説明箇所を覚え直し、解き方がわからない場合は解法を覚え直す
解法を覚えたら最後まで自力で解けるかもう一度解いてみて、解けるようになるまで繰り返す
自力で解けるようになれば、次の問題に進んで同様の作業を行う
自分が習得したい問題すべてが◯3つになれば、その参考書の解法パターンは頭に入っていることになります。
ここまでの流れが習得できれば、模試での数学偏差値が60前後まで伸びます。
ここまでの手順は「解法パターンを知識として身につける」工程でした。ここからは「身につけた解法パターンを組み合わせる」工程、いわゆる応用力を身につける工程になります。

ようやく原理の根本理解と応用練習が必要な段階にきたね
よく、基礎ができなくても応用ができれば二次試験で点数が取れると勘違いしている受験生がいますが、応用は基礎ができていなければ身につくことはありません。
なぜかというと、問題に対して解法Aだけでも解けるのが基礎問題、問題に対して解法Aと解法B両方を用いないと解けないのが応用問題という構造になっているからです。
つまり、基礎知識の完全定着こそが応用力につながるというわけですね。
では、基礎知識の完全定着とはどういう状態か。それが、以下の3つの条件すべてをクリアしているかどうかになります。
1. 解法パターンが身についているか
解法パターンについては、すでにここまでの過程で身についているのであまり気にしなくて構いません。
2. 類題の問題でも自力で解けるか
類題が解けるかどうかについては、終わらせた参考書と同レベルの参考書、あるいは同じ参考書内の類題を演習することで確認することができます。
3. 他人にわかりやすく説明できるか
じつは、この過程が多くの受験生の悩みポイントになっています。理解している状態なのかどうか、自分ではなかなかわかりづらいため、できている気になったまま放置してしまうからです。
そんな時に客観的に判断する方法が、他人に解法をわかりやすく説明できるかどうか。
ただ、説明する相手がいないという人もいると思います。そんな時は、自分自身が講師役と生徒役の一人二役になって、自分自身に説明してみてください。
- 講師役:解法の理由を説明する
- 生徒役:「なぜ」と聞き返す
これを繰り返していると、自分が理解できていない内容が浮き彫りになるので、嫌でも根本からの理解が進みやすくなります。

基本的には参考書を前から順に勉強するというやり方で問題ないですが、以下の点に気をつけてください。
数学IA
データの分析
配点が低く範囲が狭いことを踏まえると後回しでも構わない
整数問題
出題されない大学も多く、難関の単元であるため、必要であっても学力がついてから対策をした方がよい
集合と論理
主に出題されるシチュエーションは共通テストであるため最初は飛ばしても可
数学IIBC
数列
Σの本質的な理解と数学的な発想力が必要になるため最初はあまり深追いしなくてもよい
ベクトル
図形の性質や図形と方程式など他単元の理解が必要になる内容のため最初はあまり深追いしなくてもよい
平面上の曲線
出題頻度が低く出題された時は難問であるケースが多いので最初は飛ばしてもよい
統計的な推測
出題されない大学も多く、範囲が狭いことを踏まえると後回しでも構わない
数学III
数学IAIIBが先
数学IAIIBの知識が絡んでくる問題が多いため数学IIIの学習はそれらの習得後に始めること

ここでは筆者が受験時に使用した数学の参考書を紹介します。
偏差値39〜58の時
| 使った参考書 | 青チャート |
| 解いた問題 | 例題★1〜★3 |
| 解き進め方 | ◯が3つつくまで反復 |
| 意識したこと | IAから順に定着させる |
青チャートは章末問題や★4〜★5以外はそれほど難易度は高くなく、解説も丁寧に書かれている網羅系参考書なので、やり込む参考書としては選択してよかったです。
ただ、本当に数学が嫌いで苦手意識が強い人の場合は、最初に取りかかる参考書としてはやや難しく感じる可能性もあるので、その場合は白チャートを選択することをオススメします。
偏差値58〜60の時
| 使った参考書 | クリアー数学 |
| 解いた問題 | 基本問題(A問題) |
| 解き進め方 | 演習をメインに進める |
| 意識したこと | 初見でも解けるか確認 |
青チャートの次にやった参考書は教科書の傍用問題集でした。これは、青チャートで身につけた解法パターンが頭に入っているかを確認する作業、つまり類題が解けるかどうかを確認する作業です。青チャート後の参考書、つまり2冊目以降の参考書は、時間効率を考え初見で解けた問題にはOKをつけ、今後解かなくてかまいません。
また、使う参考書自体はここで挙げているクリアー数学でなくとも構いません。皆さんが持っている学校の演習用問題集で確認作業をしてみてください。
偏差値60〜64の時
| 使った参考書 | 1対1対応の演習 |
| 解いた問題 | 例題のみ |
| 解き進め方 | 演習をメインに進める |
| 意識したこと | 解けない問題は反復 |
類題演習の後に学習する参考書は上位の大学を目指す人だけで十分です。もし上位の大学を目指す受験生は、1対1対応レベルまでは確実に解けるようにしておきたいですね。
偏差値64〜70の時(筆者の時代)
| 使った参考書 | 大学への数学(黒) |
| 解いた問題 | 例題のみ |
| 解き進め方 | 演習をメインに進める |
| 意識したこと1 | 解けない問題は反復 |
| 意識したこと2 | 1問に多く時間を使う |
難関レベルの演習については、筆者の場合は大学への数学(黒)を選択しましたが、かなり古い参考書なので皆さんの場合はやさしい理系数学や文系プラチカのような参考書を使ってください。
難関の参考書を扱うレベルになると、いかに発想力を鍛えるかが勝負です。なので、これまでのように解法を頭に叩き込むのではなく、じっくり考えて1問あたりに時間を使って「考える力」を鍛えましょう。
偏差値64〜70の時(今ならコレ)
| 理系向け参考書 | やさしい理系数学 |
| 文系向け参考書 | 文系良問プラチカ |
| 解き進め方 | 演習をメインに進める |
| 意識すること1 | 解けない問題は反復 |
| 意識すること2 | 1問に多く時間を使う |
これらの参考書は、実際の難関二次問題で出されるような良質な難問揃いです。これまでの参考書のように「解法パターンを身につける」という目的で取り組む参考書というよりも、身につけてきた解法パターンの知識をもとに、いかに喰らいつけるかを確かめる参考書です。
1問あたりに20〜30分ほど考え込む時間を設けてもよいので、思考してなんとか喰らいつく練習を積み重ねましょう。また、別解や解説が豊富なので、もし自力で解けなかった場合でも、解答を見て自分なりに理解し、何度も血肉となるまで繰り返すことが大切です。
難関理系の+α参考書
東大・京大・東工大・阪大・早慶の理工・難関医学部などの難関大学を狙う受験生の場合は、時間があれば以下の参考書に触れておくと、難関大学の入試でよく出る単元の設問にも問題なく対応することができるようになります。1冊1冊が重厚なので、時間がある場合にできる量をピンポイントで進めてみてください。
| 解き進め方 | 演習と理解促進が目的 |
| 意識すること1 | 苦手な系統を中心に触れる |
| 意識すること2 | 1問に多く時間を使う |
| 意識すること3 | 解説理解と考察に時間を使う |
最後にですが、+αの参考書を除くところまでで十分どのレベルの大学でも合格ラインは狙える実力が身につくので、あとは自身の大学の過去問分析と演習を重ねて、志望大学の応用のクセに対応できるようにしておいてください。ここまでできれば、数学に関しては十分です。
テスト直しは非常に重要です。今日書いた内容の中で最も大切な内容と言っても過言ではありません。もしテスト直しをおろそかにすると、どんなに参考書演習を重ねていようと、途中で成績が伸び悩む段階がやってきます。
なぜなら、どこが自分の弱点なのかがわからないまま勉強時間をかけることになるからです。テスト結果は等身大の自分を写してくれる鏡。必ず行うようにしましょう。
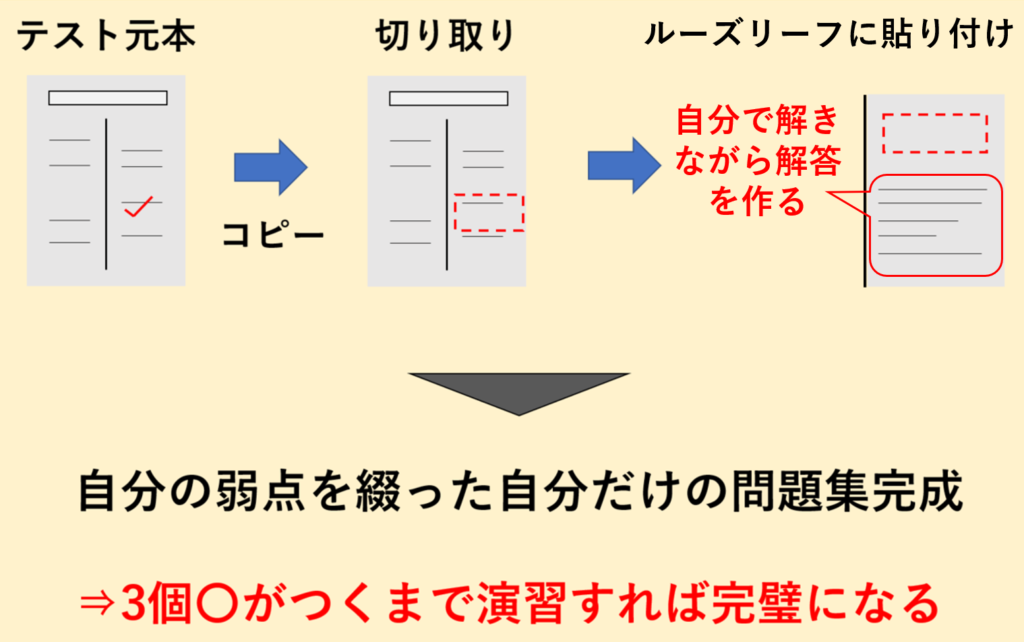
テストの直し方でおすすめの方法はこちら
受け終わったテストの問題用紙を印刷する
間違えた箇所の問題文を切りテスト直し用ノートに貼る
自分の言葉でコメントをつけ加えながら解答を作る
弱点の問題が詰まった自分だけの苦手克服ノートができあがる
以上が、学年最下位だった筆者が、理工系最難関と言われる東工大(東京科学大学)に合格した数学の勉強法です。数学は努力で克服できる科目なので、ぜひ実践して数学を苦手から得意に変えてくださいね。



